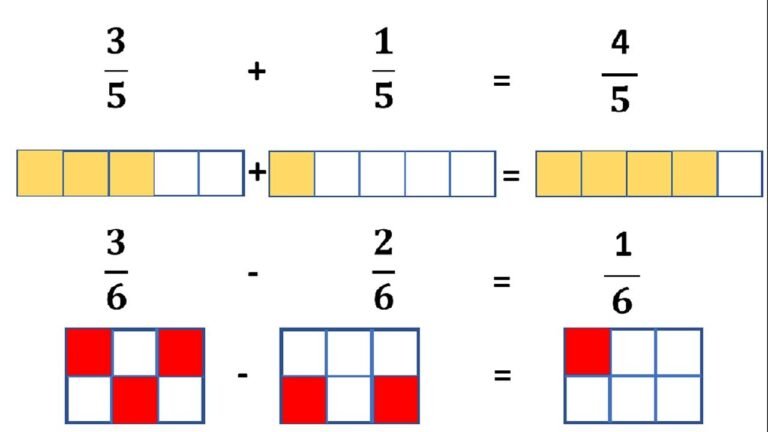
✅ Sumar fracciones con el mismo denominador es simple: sumá los numeradores y mantené el denominador; ¡ideal para cálculos rápidos y precisos!
Sumar fracciones con el mismo denominador es una de las operaciones más sencillas dentro del álgebra básica. Para realizar esta suma, simplemente se debe conservar el denominador y sumar los numeradores. Esto significa que si tenemos dos fracciones con igual denominador, como 1/5 y 2/5, el resultado será (1+2)/5 = 3/5.
En este artículo te explicaremos de forma detallada y práctica cómo sumar fracciones con el mismo denominador de manera rápida y sin errores. Además, te daremos ejemplos fáciles que te ayudarán a entender mejor la mecánica de esta operación y algunos consejos para simplificar los resultados si fuera necesario.
¿Cómo se suman fracciones con el mismo denominador?
El procedimiento es muy simple y consta de dos pasos fundamentales:
- Suma los numeradores: Se suman directamente los numeradores de las fracciones, ya que al tener igual denominador, representan partes iguales.
- Mantén el mismo denominador: El denominador permanece inalterado porque la unidad en que se divide la fracción es la misma.
Por ejemplo, para sumar 3/8 + 4/8:
- Suma los numeradores: 3 + 4 = 7
- Mantén el denominador: 8
Resultado: 7/8
¿Qué pasa si el resultado puede simplificarse?
Luego de sumar, es importante verificar si la fracción resultante puede simplificarse para obtener una forma más sencilla. Para esto, se busca un número que divida tanto al numerador como al denominador. Por ejemplo, si al sumar obtenemos 6/8, podemos simplificarla dividiendo ambos números por 2:
- Numerador: 6 ÷ 2 = 3
- Denominador: 8 ÷ 2 = 4
La fracción simplificada es 3/4, que es más fácil de interpretar.
Consejos para sumar fracciones con el mismo denominador
- Verifica siempre que los denominadores sean iguales antes de sumar.
- Suma únicamente los numeradores, no cambies el denominador.
- Simplifica el resultado para obtener una fracción más clara.
- En caso de que el numerador sea mayor que el denominador, convierte la fracción impropia en número mixto para facilitar su comprensión.
Paso a paso para resolver sumas de fracciones con igual denominador
Sumar fracciones con igual denominador es una de las operaciones más básicas pero fundamentales en el aprendizaje de las matemáticas. Comprender este proceso facilita el manejo de fracciones en problemas cotidianos y académicos.
¿Por qué es importante que los denominadores sean iguales?
El denominador indica en cuántas partes iguales se divide el entero. Cuando sumamos fracciones con el mismo denominador, estamos sumando partes del mismo tamaño, lo que simplifica la suma a solo sumar los numeradores. Por ejemplo:
- Si sumamos 3/8 + 2/8, ambas fracciones están divididas en 8 partes iguales.
- Entonces, simplemente sumamos los numeradores: 3 + 2 = 5.
- El resultado es 5/8, manteniendo el mismo denominador.
Pasos detallados para sumar fracciones con igual denominador
- Verificar que los denominadores sean iguales. Si no lo son, se debe encontrar un denominador común antes de sumar.
- Suma los numeradores: Solo sumá la parte superior de cada fracción.
- Mantén el denominador: El número de abajo permanece igual.
- Simplifica la fracción si es necesario: Dividí el numerador y denominador por su máximo común divisor (MCD).
Ejemplo práctico
Imaginemos que tenés las siguientes fracciones para sumar:
- 7/12
- 3/12
Procedimiento:
- Los denominadores son iguales (12).
- Sumamos los numeradores: 7 + 3 = 10.
- Mantenemos el denominador: 12.
- La suma es 10/12.
- Finalmente, simplificamos dividiendo por 2 (el MCD de 10 y 12):
- 10 ÷ 2 = 5 y 12 ÷ 2 = 6.
- Resultado final: 5/6.
Consejos prácticos para sumar fracciones con denominadores iguales
- Siempre verificá los denominadores: Asegurate que sean iguales antes de sumar.
- Usá papel y lápiz o herramientas digitales: Para evitar errores, anotá bien los numeradores y denominadores.
- Recordá simplificar: Esto te ayudará a obtener resultados más claros y fáciles de interpretar.
- Practica con ejemplos cotidianos: Por ejemplo, sumá porciones de pizza, fracciones en recetas de cocina o tiempos en minutos.
Tabla resumen del proceso
| Paso | Acción | Ejemplo |
|---|---|---|
| 1 | Verificar denominadores | 3/8 y 2/8 (denominadores iguales) |
| 2 | Suma numeradores | 3 + 2 = 5 |
| 3 | Mantener denominador | 8 |
| 4 | Simplificar fracción | 5/8 (ya simplificada) |
Casos de uso y aplicaciones cotidianas
La suma de fracciones con igual denominador aparece en recetas de cocina, donde diferentes ingredientes se miden en fracciones. También es común en el cálculo de tiempos, por ejemplo, sumar minutos de una actividad a otra. Incluso en el diseño gráfico o construcción, donde las medidas a menudo se representan en fracciones con mismo denominador.
Preguntas frecuentes
¿Qué es una fracción con el mismo denominador?
Son aquellas fracciones que tienen el mismo número en la parte inferior, llamado denominador.
¿Cómo se suman fracciones con igual denominador?
Se suman solo los numeradores y se mantiene el mismo denominador.
¿Se puede simplificar la fracción después de sumar?
Sí, siempre conviene simplificar para obtener la fracción más simple.
¿Qué pasa si la suma da un número mayor que el denominador?
La fracción puede convertirse en un número mixto o un entero si es divisible.
¿Es necesario encontrar un común denominador en estos casos?
No, porque ya tienen el mismo denominador, por eso es más fácil sumarlas.
¿Puedo sumar fracciones con diferente denominador sin convertirlas?
No, primero hay que encontrar un denominador común antes de sumar.
| Punto clave | Descripción |
|---|---|
| Denominador | Parte inferior de la fracción, debe ser igual para sumar directamente. |
| Numerador | Parte superior que suma entre fracciones con mismo denominador. |
| Suma directa | Se suman los numeradores y se mantiene el denominador igual. |
| Simplificación | Reducir la fracción resultante dividiendo numerador y denominador por su mcd. |
| Fracción impropia | Si el numerador es mayor que el denominador, puede ser convertida en número mixto. |
| Ejemplo básico | 1/5 + 2/5 = 3/5 |
¡Dejá tus comentarios abajo y no te olvides de revisar otros artículos en nuestra web que te pueden interesar para seguir aprendiendo sobre matemáticas!